How To Convert From Decimal Number To Binary Number

The computer was built with the ability to understand the binary numbers. Meanwhile, the human use the decimal numbers to perform the mathematical operations, eg: addition, subtraction, multiplication, division etc. So here, we can see the significant differences between the human and the computer. This differences are refer to the numbering systems which used by both parties. However, we often find that the human (as the computer’s user) depend on the computer to carry out the certain tasks, eg: writing the documents, perform mathematical operations etc.

I personally see, the human dependence on the computer may arouse the compatibility issue between both of them. This compatibility issue is about how the computer can manage the human’s data, eg: decimal numbers, whereas the computer only can understand the binary numbers.

Through this article, I will try to answer this question by describing about the binary numbers and little explanations about the decimal numbers. Within this article, I will also explain the steps how to convert from decimal number to binary number. I think this conversion process is applied by the computer when managing the human’s data which enter into its system. 


The description about the binary numbers



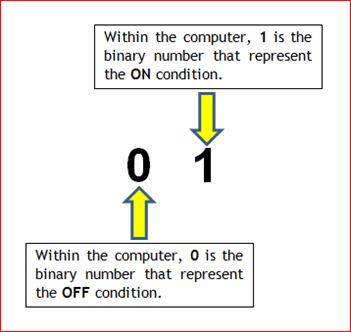
Within the above picture, we can see the 2 different numbers which respectively are 0 and 1. Both of these numbers (0 and 1) are the binary numbers which by default, include in the base-2 numbering system.

The binary numbers had plays the significant role within the field of computing. Because the binary numbers only consists of the 2 different numbers, so it is easier to use them as the values to represent the logical conditions. By default, both of these values (the binary numbers) represent the logical conditions based on the following methods:

• The binary 0 is assigned to the logical condition OFF.
  
• The binary 1 is assigned to the logical condition ON.

The computer system use the digital signal to represent data and information. Meanwhile, the digital signal has only 2 discrete conditions that can be represented logically as ON and OFF. The ON condition is means the positive voltage level and the OFF condition is means the zero voltage level. Because the binary numbers only have two numbers, so they can be the most suitable numbers to represent the logical conditions (ON and OFF) on the digital signal. Usually, the logical conditions on the digital signal will be represented using the methods listed above.





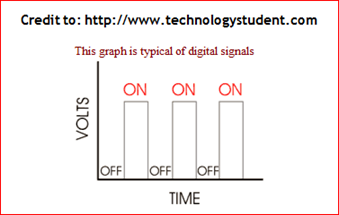
How the computer see the human’s data?
As I previously mentioned, the computer use the digital signal to represent data and information. Meanwhile the logical conditions on the digital signal is represented using the binary numbers. However, the computer do not see human’s data in form of the digital signal. It usually see the human’s data in form of  the sequence of binary numbers with 8-bits values as shown within the picture below:

The picture above presents us the sequence of binary numbers which represent the data and information viewed by the computer system. What we can conclude about this picture are as follows:

• The single bit of data is the smallest size of data which the computer can process. It can has either the binary number 0 (represent the OFF condition) or the binary number 1 (represent the ON condition). However by default, the computer does not process just the single bit of data at a time. For the purpose of performance, the computer will process data in the sequence of binary numbers that equal to 8-bits of data at a time. For your information, the early computer can process the 8-bits of data at a time. But nowadays, the modern computer can process the 64-bits of data at a time.
  
  
• The 8-bits of data is equal to 1-byte of data, the 16-bits of data = 16/8 is equal to 2-bytes of data, the 32-bits of data = 32/8 is equal to 4-bytes of data, and the 64-bits of data = 64/8 is equal to 8-bytes of data. I think most of us are familiar with these bits and bytes’ values.
  
  
• The 8-bits of data can represent 256 decimal numbers which can have the range of values from 0 to 255.Eg: 00000000 = 0 (the decimal number), 11111111 = 255, 10101010 = 170.
  
  
• To translate the value of the 8-bits of data to the decimal number (human’s data), every single bit of data within the 8-bits of data must be paired with every single bit position. The bit positions have the range of numbers from 0 to 7. The arrangement of bit positions that paired together with every single bit of data within the 8-bits of data, can be described using the table below:
  
   
  
  Based on the table above, the numbers from 0 to 7 that represent the bit positions are the exponent numbers that become “power to the base number 2”. The number 2 is selected as the base number because the binary numbers have 2 numbers. The example below will enhance your understanding about the exponent numbers that become “power to the base number 2”:
  
  2⁰, 2¹, 2², 2³, 2⁴, 2⁵, 2⁶, 2⁷
  
  
  Below is the complete description related to the above examples:    
  
  
  
  When you perform the mathematical exponentiation on the base numbers above you will get the decimal values like within the following table:
  
  
  
  You will use the above table when you want to find out the binary values (8-bits of data) that equivalent to the decimal numbers which had been given to you. The decimal numbers will have the range of decimal values from 0 to 255. You will learn more about this in the next section entitled how to convert the decimal number to the binary number?

The brief description about the decimal numbers 
The human use the decimal numbers when perform the mathematical calculations. The decimal numbers is the group of numbers which form the base-10 numbering system. The base-10 numbering system consists of 10 numbers like the following:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Among the decimal numbers listed above, we can combine them to form a decimal number with larger value, for the example, we can combine the decimal numbers 3, 4, 5 and 6 to form a decimal number with value, 3456 which can be read as THREE THOUSANDS AND FOUR HUNDREDS AND FIFTY SIX.



How to convert the decimal number to the binary number?
If the computer’s user type the decimal number, how that number will look like in “the eyes of computer”? In order to answer this question, we need to learn how to convert the decimal number into the binary number.

Let say the computer’s user type the decimal number 22 on the Notepad program. By default, the computer system will view this number as the sequence of binary numbers with the 8-bits of data. So now, from this issues, the some simple questions can be raised:

• How the patterns of the sequence of binary numbers with the 8-bits of data equivalent to the decimal number 22 will look like in “the eyes of computer”?
  
• How many binary numbers 0 and 1 will appear within the 8-bits of data?
  
• In which bit positions, both of the binary numbers will be paired within the 8-bits of data?

To answer the above questions, we should perform the following steps which will also teach us how to convert the decimal number to the binary number:

1. First of all, we need to construct a table that contains the bit positions (the range of numbers from 0 to 7) together with the decimal numbers that assigned to every bit position. Look the table below:  
   
    
   
   From the table above, we can raise the following question:
   
   How the decimal numbers that paired to every bit position were determined?
   
   To answer the above question, we need to create the table similar to the above. Then we add one row that contains the sequence of binary numbers (8-bits of data). All the binary numbers within this row must have the binary number 1. See the following table: 
   
    
   
   Now, based on the above table, you can determine the decimal number for every bit position (remember, the bit position is the exponent number that become “power to the base number 2”) by performing the following mathematical operation (multiplication process): 
   
   MULTIPLY the binary number (1) with the base number 2 power by the bit position. Eg: 1 * 2⁰, 1 * 2¹, 1 * 2², 1 * 2³, 1 * 2⁴, 1 * 2⁵, 1 * 2⁶, 1 * 2⁷.
   
   For more details information about the examples above, see the description below:  
   
   
   
   THE IMPORTANT TASK FOR STEP 1:
   In this first step, the most important task that we have to do is to determine the decimal numbers that paired with every bit position.
   
   
2. At this point, I hope you can understand what I try to deliver within the previous step (step 1). Now, you had acquire the table that display the bit positions (0 – 7) together with the decimal numbers. These numbers are produced from the mathematical operation which had been performed within the step 1.
   
   Now, in this step, we will perform the mathematical operation (the addition process) onto the decimal numbers within the table as shown below in order to get the decimal number 22 as the final amount:
   
    
   
   Based on the table above, we should perform the addition process onto the decimal numbers within the red cells. So, the process will look like the following:
   
   16 + 4 + 2 = 22    
   
   THE IMPORTANT TASK FOR STEP 2:
   Within this step, the most important task is we need to determine every decimal number involved within the addition process which will produce the desired decimal number (in this case is 22) as the final amount. In this case, the decimal numbers involved are 16, 4 and 2.
   
   
3. In the previous step (step 2) we had determine the decimal numbers which involved in the addition process in order to get the decimal number 22 as the final amount. They are numbers 16, 4 and 2 which are inside the red cells within the table shown below:
   
   
   
   So now, within this step and beyond, we will answer all the questions which had been raised regarding this issue. Before we proceed this step, it is good to recall those questions: 
   
   
   
   To answer all the questions above, we need to use the above table. Then, we add one more row within this table This row represent the row of binary number. So that we will get the following table:
   
   
   
   Then, within the row of binary number, we need to fill the suitable binary number into all of its cells. These binary numbers can be either 0 or 1 as long as this sequence of binary numbers (8-bits of data) is equal to the decimal number 22.
   
   Now, based on the row of binary number within the table above, we will fill up the binary number 1 into the cells that locate below the red cells (contains the decimal numbers 16, 4 and 2). See the table below:
   
   
   
   The reason, why we should fill the binary number 1 within these cells is based on the previous mathematical operation (multiplication process) within the step 1. For the example, if we want to produce the decimal number 16, we need to perform the following multiplication process: 
   
   MULTIPLY the binary number 1 with the base number 2 power by the number of bit position 4. Eg: 1 * 2⁴ = 1 * 16 = 16
   
   Logically if we fill the binary number 0 within the cell below the red cell that contains the decimal number 16, we will return the decimal number 0 as the final result. The following multiplication process will enhance you understanding about what I said:
   
   MULTIPLY the binary number 0 with the base number 2 power by the number of bit position 4. Eg: 0 * 2⁴ = 0 * 16 = 0
   
   THE IMPORTANT TASK FOR STEP 3:
   Within this step, the most important task is we need to fill up the certain cells belong to the row of binary number with the binary number 1. The purpose of this task is to produce some decimal numbers (in this case is the numbers 16, 4 and 2) which when we totalize them, we will get the desired decimal number (in this case is the number 22) as the final amount.
   
   
4. This is the final step which can be the easiest step. So far, you had determine and fill up the binary number 1 into the related cells belong to the row of binary number. See the table below:
   
   
   
   Now in this step, you will fill up the remaining cells (empty cells) with the binary number 0 within the row of binary number as shown within the table above. After we fill up all these cells, the sequence of binary numbers (that contains the 8-bits of data) will formed. See the row of binary number (contains the light blue cells) within the table below:
   
   
   
   If we take out and rearrange this sequence of binary numbers (inside the light blue cells) within the above table, we will see the following patterns of the 8-bits of data:
   
   00010110 = 22
   
   So, if the people ask you what is the value of 8-bits of data that equal to the decimal number 22? The answer in the sequence of binary number with 8-bits of data will be 00010110.
   
   THE IMPORTANT TASK FOR STEP 4:
   Within this step, the most important task is we need to fill up the remaining cells within the row of binary number with the binary number 0. When this final step is accomplished, we will get the sequence of binary numbers (that contains the 8-bits of data) that equal to the desired decimal number. In this case we get the 8-bits of data, 00010110 that equal to the decimal number 22.